Teng Ma

Teng Ma

Variational Autoencoder explained

11 minute read

Published:

Variational Autoencoders (VAEs) are a powerful class of generative models used in unsupervised learning, combining the strengths of both neural networks and probabilistic models. They aim to approximate an underlying latent space that represents the distribution of data. To achieve this, VAEs learn to encode high-dimensional input data into a lower dimensional set of latent variables using a variational inference process. By doing so, they can reconstruct the original input while also enabling manipulation and generation of new samples within the learned distribution. This is particularly useful for applications like image synthesis, where the ability to encode complex data and then decode it as new variations of that data is crucial.

Autoencoder

Autoencoder is an encoder-decoder structure nerual network, aims to learn a compressed representation of the data during encoding (also referred as feature extraction), and from which generate new data (reconstruct input) similar as possible to the original data. The formal definition [2]: Autoencoder is to learn the functions $A: R^n -> R^p$ (encoder) and $B: R^p -> R^n$ (decoder) that satisfy \(argmin_{A,B}E[\Delta (x,B A(x))],\) where $\Delta$ is the loss function that measures the distance between the output generated from the decoder and the input, $E$ is expectation, $B A(x)$ is the autoencoder output.

A generalization of PCA? Note: In speaking of dimention reduction of data, one may think about Principal Component Analysis (PCA), which represent data using a low dimensional hyperplane (find a set of orthogonal basis). A linear autoencoder achieves the same result as PCA, but in practice we add non-linearity to encoder nerual network (also decoder), so the autoencoder learns a non-linear manifold instead.


Variational Bayesian Inference

Basiclly, Bayesian Inference works in this way: first we choose a prior distribution over the unknown parameters or latent variables, then update it to a posterior distribution after seeing data. Variational Inference (VI) is an approach to obtain the posterior distribution by finding a surrogate distribution that approximates the true distribution. Another well-known way to calculate a posterior is MCMC, which tries to sample data from the posterior, usually computationally expensive(so slower than VI, but more accurate).

Bayesian Inference Recall the Bayes' Rule: $$ p(b|a)=p(a|b)P(b)/p(a) $$ Assume $p(\theta)$ is a marginal distribution over model parameters $\theta$, i.e. a prior distribution. $p(D|\theta)$ is the According to the chain rule in probability, we have: $$ p(\theta,D)=p(\theta|D)p(D)=p(\theta)p(D|\theta) $$ Note that $p(D)$ is a constant, the posterior distribution over $\theta$ is: $$ p(\theta|D)=\frac{p(\theta)p(D|\theta)}{p(D)} \propto p(\theta)p(D|\theta) $$ That's the Bayes' Rule. $D$ here refers to the dataset consists of $n$ independently and identically distributed (i.i.d) observed datapoints ${x_1,x_2,...,x_n} \in D$. For convenience, $p(D|\theta)$, the likelihood of $D$ under model parameter $\theta$ (or the probability assigned to the data under the model with parameters $\theta$) is written as $p_\theta(D)$. We commonly use maximum log-likelihood to estimate $\theta$: $$ logp_\theta (D)=\sum_{x \in D}log p_\theta(x) $$ The aim is to search for a value of $\theta$ that makes $p_\theta(x)$ approaches to the true distribution $p^*(x)$. Then we can use Bayes' Rule to make prediction about new data $x_{new}$: $$ p(x=x_{new}|D)=\int p(x=x_{new},\theta|D)d\theta = \int p(x=x_{new}|\theta)p(\theta|D)d\theta $$


In more complex cases, such as image generation, the model is parameterized with neural networks, and is not fully observed. We call such models deep latent variable model (DLVM), and variables that is not observed latent variables $z$ (e.g. encoded representation in autoencoders). We assume that the observed variables $x$ can be explained in terms of latent variables $z$: \(p_\theta(x)=\int p_\theta(x,z)dz=\int p_\theta(x|z)p(z)dz\) However, the marginal probability of data under the model $p_\theta(x)$ is intractable in DLVMs, since there’s no analytic solution or efficient estimator for the integral (hard to compute for high dimentional variables). Note that $p_\theta(x,z)$ is tractable and easy to compute. A tractable marginal likelihood $p_\theta(x)$ leads to a tractable posterior $p_\theta(z|x)$, and vice versa.
Variational inference approximates the $p_\theta(z|x)$ and $p_\theta(x)$ using parametrised distributions (e.g. Gaussian) by minimize an error (e.g. Kullback-Leibler divergence) between the approximation and target distribution. Now the inference is converted to an optimization problem. We find that minimizing the K-L divergence is equivalent to maximizing the ELBO (Evidence of Lower Bound), the derivation is given in the next section. One way to maximize ELBO is to assume independency between different dimentions of $z$ (mean-field theory) and proceed in a closed form optimization (coordinate ascent variational inference). While VAE takes another approach that is suitable for large dataset in deep neural networks, Stochastic Gradient Variational Bayes estimator, and you will see how it works in the next section as well.
From the perspective of functional analysis, both K-L divergence and ELBO are functional we want to find extreme points, find more below if you are interested in the mathematics.

Calculus of Variations Variation is commonly used in finding the extreme value of a functional, e.g. finding a brachistochrone curve, or curve of fastest descent, which can be analogous to the derivation of ordinary functions. In mathematics, a functional is a special function that takes functions as input and output scalar numbers, a mapping from vector space to scalar domain (a function can be regarded as an infinite-dimensional vector). A simplest functional: $\int_a ^b f(x) dx$, input a function $f(x)$ and yield the area under the curve of $f(x)$ between $x=a$ and $x=b$. The output area depends on how $f(x)$, or the curve looks like. To put it in a more generalized way, a functional $I(y)$ can be like: $$ I(y)=\int_a ^b F(y,y';x)dx $$ Where $y,y'$ are functions of $x$, and here just write a first order derivative (there maybe higher order of derivatives). Usually $\delta$ is used to denote variation, e.g. $\delta y$ is the variation of $y(x)$, which means a tiny (infinitely small) change in $y(x)$ when $x$ remain unchanged. Note that $\delta y$ is caused by changes in the form of $y$, not $x$, since $dx$ here is supposed to be 0 (differ from derivative $dy$). The extreme value of $I(y)$ happens when $\delta I=0$, the same way we determine the extreme value of a function (the first order derivative of $\frac{df(x)}{dx}=0$, which could be explained in this way: near the extreme point, $f(x)$ remain unchanged when applying small changes to $x$). Introduce a differentiable function $h(x)$ as the increment of $y(x)$, $h(x)$ satisfies the boundary constraints $h(a)=h(b)=0$, $$ \begin{aligned} \delta I = I(y+h)-I(y) &= \int _a^b [F(y+h,y'+h';x)-F(y,y';x)]dx\\ &= \int _a^b [F_y(y,y';x)h+F_{y'}(y,y';x)h']dx +o(h^2) \\ &= \int _a^b [\frac{\partial F}{\partial y}-\frac{d}{dx}(\frac{\partial F}{\partial y'})]hdx+\frac{\partial F}{\partial y'}h |_{x=a}^{x=b}+o(h^2) \end{aligned} $$ the second line of the equation is derived by Taylor expansion of $F(y+h,y'+h';x)$, the third line is obtained using integration by parts. Since $\frac{\partial F}{\partial y'}h |_{x=a}^{x=b}=0$ and the hiher order term $o(h^2)$ is neglectable, if $\delta I=0$, the following equations exists: $$ \frac{\partial F}{\partial y}-\frac{d}{dx}(\frac{\partial F}{\partial y'})=0 $$ Yes, it's E-L equation.


Variational Autoencoder

Let’s interpret VAE from a perspective of Bayesian inference. The encoder is an inference model $q_\phi (z|x)$ that obtains the compressed representation i.e. latent variables $z$ given observed variables $x$. The decoder $p_\theta (x|z)$ decode data from $z$ space back to $x$ space.
VAE
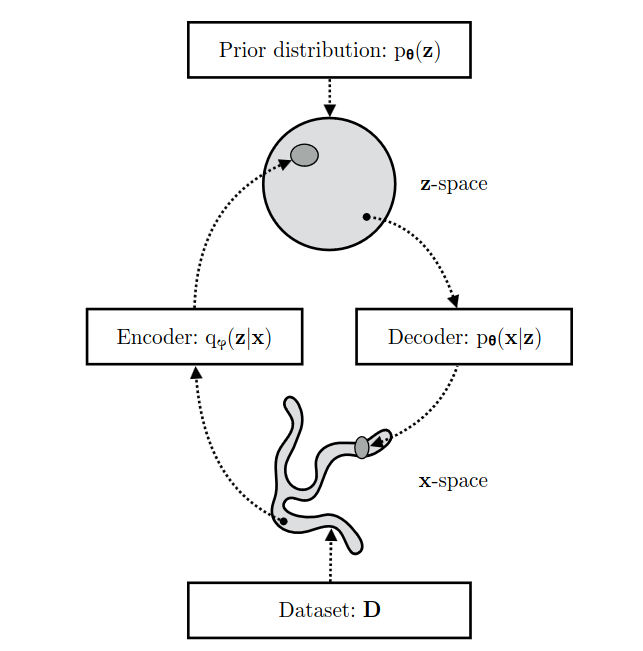
A VAE learns stochastic mappings between the observed x-space and a lantent z space. $\phi$ is the parameters of the encoder, and $\theta$ is the parameters of the decoder. $\theta$ is optimized to make the generated data more compatible with the distribution of real data; $\phi$ is optimized so that the encoder $q_\phi (z|x)$ approximates the true but intractable posterior $p_\theta (z|x)$ of the generative model.

\(q_\phi (z|x) \approx p_\theta (z|x)\)
We know that Kullback–Leibler divergence measures the distance of two distributions. Given two continuous distributions’ PDF $p(z)$, $q(z)$, the K-L divergence is defined as:
\(D_{KL}(q||p)=\int q(z)log(\frac{q(z)}{p(z)})dz\)

In practice, we choose evidence lower bound (ELBO) as the optimization objective of variational methods including VAE. See the following derivation.
\(\begin{aligned} logp_\theta(x)&=E_{q_\phi (z|x)}[logp_\theta(x)]\\ &=E_{q_\phi (z|x)}[log[\frac{p_\theta(x,z)}{p_\theta(z|x)}]]\\ &=E_{q_\phi (z|x)}[log[\frac{p_\theta(x,z)}{q_\phi (z|x)} \frac{q_\phi (z|x)}{p_\theta(z|x)}]]\\ &=E_{q_\phi (z|x)}[log[\frac{p_\theta(x,z)}{q_\phi (z|x)}]]+E_{q_\phi (z|x)}[log[\frac{q_\phi (z|x)}{p_\theta(z|x)}]] \\ &=L_{\theta,\phi}(x)+D_{KL}(q_\phi (z|x)||p_\theta (z|x)) \end{aligned}\)

From the equations above, we know that given a $p_\theta (x)$, maximizing ELBO is equivalent to minimizing K-L divergence, since the KL divergence between $q_\phi (z|x)$ and $p_\theta (z|x)$ is non-negative (equal to 0 if, and only if two distributions are equal).
\(\begin{aligned} L_{\theta,\phi}(x)&=logp_\theta(x)-D_{KL}(q_\phi (z|x)||p_\theta (z|x)) \\ &\leq logp_\theta(x) \end{aligned}\)

$L_{\theta,\phi}(x)$ is called variational lower bound, aka evidence lower bound (ELBO):
\(L_{\theta,\phi}(x)=E_{q_\phi (z|x)}[logp_\theta(x,z)-log q_\phi (z|x)]\)

We now see why choosing ELBO over KL divergence: in ELBO, we deal with the joint distribution $p_{\theta}(x,z)$ and posterior of inference model $q_\phi(z|x)$ ( which is tractable because we can choose the surrogate model), tactically avoid the intractable posterior $q_{\theta}(z|x)$ in generative model. Notably, maximizing ELBO w.r.t. $\theta$ and $\phi$ will not only minimize KL divergence of $q_\phi (z|x)$ from $p_\theta (z|x)$, but also maximize $p_\theta(x)$, which means both the inference model (encoder) and the generative model (decoder) get better.
The (unbiased) gradient of ELBO w.r.t. all parameters ($\phi$ and $\theta$) can be optimized using stochastic gradient descent (SGD). For $\theta$, we have:
\(\begin{aligned} \nabla_\theta L_{\theta,\phi}(x) &= \nabla_\theta E_{q_\phi (z|x)}[logp_\theta(x,z)-log q_\phi (z|x)]\\&=E_{q_\phi (z|x)}[\nabla_\theta(logp_\theta(x,z)-log q_\phi (z|x))]\\ & \simeq \nabla_\theta logp_\theta(x,z) \end{aligned}\)

So we can simply sample $z$ from $q_\phi (z|x)$ using Monte Carlo estimator. However, to get the gradient of ELBO w.r.t. $\phi$, we need a reparameterization trick that let $z$ be a function of $\phi,x$ and a random variable $\epsilon$. We cannot follow the same method as we did for $\theta$, because $q_\phi (z|x)$ is a function of $\phi$, the equation is not valid:
\(\begin{aligned} \nabla_\phi L_{\theta,\phi}(x) &= \nabla_\phi E_{q_\phi (z|x)}[logp_\theta(x,z)-log q_\phi (z|x)]\\& \neq E_{q_\phi (z|x)}[\nabla_\phi(logp_\theta(x,z)-log q_\phi (z|x))] \end{aligned}\)

After introducing $\epsilon$, the ELBO is rewritten as:
\(\begin{aligned} L_{\theta,\phi}(x) &= E_{q_\phi (z|x)}[logp_\theta(x,z)-log q_\phi (z|x)] \\ &= E_{p(\epsilon)}[logp_\theta(x,z)-log q_\phi (z|x)] \end{aligned}\)

where $z = g(\epsilon, \phi, x)$, and we can use Monte Carlo estimator to get $\nabla_\phi L_{\theta,\phi}(x)$ by sample random noise $\epsilon \sim p(\epsilon)$.

Reparameterization trick Since we cannot compute gradients of the objective $f$ w.r.t. $\phi$ through the random variable $z \sim q_\phi (z|x)$, we can re-parameterizing $z$ as a deterministic and differentiable function of $\phi, x$, and a random variable $\epsilon$. In this way, we externalize the randomness in z by introducing $\epsilon$ (random noise) that is independent of $x$ or $phi$. We usually know the pdf of $p(\epsilon)$, e.g. we choose normal distribution for $\epsilon \sim N(0, I)$. $$ z = g(\epsilon, \phi, x) \\ E_{q_\phi (z|x)}[f(z)] = E_{p(\epsilon)}[f(z)] $$ Now we can use a simple Monte Carlo estimator to get the unbiased estimation of the gradients: $$ \begin{aligned} \nabla_\phi E_{q_\phi (z|x)}[f(z)] &= \nabla_\phi E_{p(\epsilon)}[f(z)] \\ &= E_{p(\epsilon)}[\nabla_\phi f(z)] \\ & \simeq \nabla_\phi f(z) \end{aligned} $$


Reference:
[1] Kingma, Diederik Pieter. “Variational inference & deep learning: A new synthesis.” (2017).
[2] Bank, Dor, Noam Koenigstein, and Raja Giryes. “Autoencoders.” Machine learning for data science handbook: data mining and knowledge discovery handbook (2023): 353-374.
[3] Bishop, Christopher M., and Nasser M. Nasrabadi. Pattern recognition and machine learning. Vol. 4. No. 4. New York: springer, 2006.
[4] Calculus of Variations (https://courses.maths.ox.ac.uk/pluginfile.php/29848/mod_resource/content/1/Notes%202022.pdf)

You May Also Enjoy

Hungarian Algorithm in multiple object tracking

7 minute read

Published:

Facilitated by the development of deep learning in subfields of computer vision including single object tracking (SOT), video object detection (VOD), and re-identification (Re-ID), many methods of multi-object tracking (MOT) have emerged, such as various embedding models designed for object locations and track identities [1]. While tracking-by-detection is still an effective paradigm for MOT, since we can always combine off-the-shelf state-of-the-art detectors and Re-ID models to improve the MOT system. The idea is: detect the objects in the current frame, then try to associate the detected boxes with tracked boxes in the previous frames. In practice, we need a more sophisticated design (e.g. choose similarity indices for data association, use Kalman Filter to predict new locations of tracks etc.) and proper strategies (e.g. to delete or initialize tracks). Hunarian algorithm is commonly used to matching objects after we get the similarity matrix, in this blog, I will try to explain how and why Hunarian algorithm works from the perspective of linear programming.

Problem Description

Hunarian algorithm or Kuhn-Munkres algorithm is well known for solving assignment problem, which involves assigning tasks to agents (or jobs to workers) such that the total cost is minimized (or the total profit is maximized), subject to the constraint that each agent is assigned exactly one task, and each task is assigned to exactly one agent.

Primal Form of the Assignment Problem

We are given an $n \times n$ cost matrix $C$, where $c_{ij}$ is the cost of assigning agent $i$ to task $j$.
\(\begin{aligned} \text{min} & \sum_{i \in I} \sum_{j \in J} c_{ij}x_{ij} \\ s.t. & \sum_{j \in J}x_{ij} = 1 \text{ for all } i \in I \\ &\sum_{i \in I}x_{ij} = 1 \text{ for all } j \in J \\ & x_{ij} \geq 0 \end{aligned}\)

Note that $x_{ij} = 1$ if i is assigned to j and 0 otherwise.

Assignment Problem is a classic linear programming problem, since both the objective function and constraints are linear sums, even though it involves binary decision variables. We can model the problem as a bipartite graph and interpret the algorithm from the perspective of graph (find the perfect matching by finding augmenting path), but this blog will not cover this topic. Let’s try to understand Hungarian algorithm under the framework of linear programming. Since the primal problem is tricky to deal with, let’s go for the dual form of the problem.

Primal to Dual To convert the primal Assignment Problem to its dual form, we need to use Lagrange multipliers to relax the equality constraints in the primal problem. Introduce $u_i$ as the Lagrange multiplier associated with the constraint that agent $i$ is assigned exactly one task ($\sum_j x_{ij} = 1$), $v_j$ as the Lagrange multiplier associated with the constraint that task $j$ is assigned to exactly one agent ($\sum_i x_{ij} = 1$), then formulate the Lagrangian:
$$ L(x_{ij},u_i,v_j)=\sum_{i=1}^n \sum_{j=1}^n c_{ij}x_{ij}+\sum_{i=1}^n u_i (1-\sum_{j=1}^n x_{ij})+\sum_{j=1}^n v_j (1-\sum_{i=1}^n x_{ij}) $$ Lagrange dual function is defined as the minimum value of the Lagrangian over primal variables:
$$ g(u,v)=\text{inf}_x L(x,u,v) $$ where $\text{inf}_x$ means the infimum (the lower bound) of the Lagrangian over $x$. Since the dual function is the pointwise infimum of a family of affine functions of (u, ν), it is concave, even when the problem is not convex [2]. To minimize this Lagrangian $L(x_{ij},u_i,v_j)$ with respect to $x_{ij}$, rewrite the Lagrangian as:
$$ L(x_{ij},u_i,v_j)=\sum_{i=1}^n \sum_{j=1}^n [(c_{ij}-u_i-v_j)x_{ij}] + \sum_{i=1}^n u_i + \sum_{j=1}^n v_j $$ The minimization occurs in the condition:
$$ x_{ij}=1 \ \text{ if }\ c_{ij} \leq u_i+v_j \\ x_{ij}=0 \ \text{ if }\ c_{ij} > u_i+v_j $$ Now we want to find the tightest lower bound or minimum duality gap, so we need to maximize the dual function w.r.t $u$ and $v$. In the case of $x_{ij}=1$ If $c_{ij} \leq u_i+v_j$, the maximum occurs when $c_{ij} = u_i+v_j$, so $c_{ij}-u_i-v_j$ in Lagrangian is non-negative.


Dual Form of the Assignment Problem

The dual form of the Assignment Problem can be written as:
\(\begin{aligned} \text{max} &\sum_{i=1}^n u_i + \sum_{j=1}^n v_j \\ s.t. & u_i+v_j \leq c_{ij}, \ \forall i, j \end{aligned}\)

where $u_i$ is the dual variable associated with agent $i$’s assignment constraint, $v_j$ is the dual variable associated with task $j$’s assignment constraint.
The strong duality theorem of linear programming guarantees that if a feasible and bounded solution exists for the primal linear problem, the dual linear problem is feasible (and bounded as well, by weak duality), with the same optimum value as the primal [3]. The primal problem has constraints that ensure every agent is assigned exactly one task, and every task is assigned exactly one agent, a feasible primal solution exists (since the problem is well-posed with the same number of agents and tasks).

Hungarian Algorithm

Given a $n \times n$ cost matrix (Adjacent Matrix in Graph theory) $C$, the algorithm is summarized as 5 steps below:

  1. Find and subtract the row minimum, namely find the minimum element in each row of the cost matrix and subtract the minimum element in each row from the element in that row.
  2. Find and subtract the colume minimum, namely find the minimum element of each column in the remaining matrix and subtract the minimum element in each column from the elements in that column.
  3. Use the minimum number of horizontal or vertical lines to cover all zero elements in the matrix. If the minimum number of lines is equal to $n$, stop running; if the minimum number of lines is less than $n$, continue to the next step.
  4. Find the minimum value among the uncovered elements, subtract this minimum value from the uncovered elements, and add this minimum value to the elements at the intersection of different lines.
  5. Go back to step 3, that is, continue to cover all zero elements in the matrix with the minimum number of horizontal or vertical lines. If the minimum number of lines is equal to $n$, stop running; if the minimum number of lines is less than $n$, execute step 4.

For details of $O(n^3)$ algorithm implementation, refer to this blog from cp algorithms, where the dual variables $u,v$ are denoted as potential. Hungarian algorithm updates the search of optimal value by continuesly increase the sum of $u,v$: \(f= \sum_{i=1}^n u[i] + \sum_{j=1}^n v[j]\)

In the context of MOT, cost matrix is filled with IOU or similarity score obtained from ReID features between objects in two consecutive frames. Sometimes the matrix is non-square, we can add dummy rows or columes with zeros and run more iterations.

Reference:
[1] Wang, G., Song, M., & Hwang, J. N. (2022). Recent advances in embedding methods for multi-object tracking: a survey. arXiv preprint arXiv:2205.10766.
[2] Boyd, Stephen, and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.
[3] Matoušek, Jiří, and Bernd Gärtner. Understanding and using linear programming. Vol. 1. Berlin: Springer, 2007.

Deploy LLMs on a phone with arm chips

4 minute read

Published:

In this blog, I’m going to share how I deployed LLMs (1~3b) and ASR models (whisper tiny & base) on my old smart phone, Xiaomi 8 (dipper). It was released in 2018, with a broken screen and depleted battery after several years of heavy usage, it still offers acceptable speed and fluency running daily light-weight apps. So I wonder, if I deploy modern machine models, such as LLMs, on the phone, and can I run the large models smoothly. Let’s see.
The hardware configuration: 8-cores CPU with 4 big cores (Cortex-A75) and 4 small cores (Cortex-A55), 64 GB storage and 6 GB RAM. It has a integrated GPU, which I didn’t find a way to utilize during model inference, so the computation is totally counted on CPU in this trial. To better leverage the power of this CPU, I uninstall the android system (MIUI 12) and port a Ubuntu touch on the phone. Basically it’s a linux OS but using the underlying andriod framework to control hardwares, and it gives me a much longer battery life compared to android, also more convenience since I am a rookie in android development. Models are quantized versions from llamacpp and whispercpp.
To get rid of the cumbersome work build an app with GUI, I run models in command line using the terminal app originally from Ubuntu touch, which can be regarded as the same terminal on Ubuntu desktop in this case. All I need to do is to compile the c++ code into an executable file that runs on my phone. Since the architecture of my laptop cpu is x86, the version of glibc, libstdc++ are different from the libs on the phone, I could either compile on the phone directly or cross compile on my PC with a specific toolchain. I kept all the heavy work on PC and built my own toolchain using crosstool-NG, which is targeted at building toolchains.

LLMs Inference speed up EP1 - kv cache

6 minute read

Published:

Large Language Models (LLMs) have revolutionized the field of natural language processing, enabling significant advancements in tasks such as language translation, text summarization, and sentiment analysis. However, despite their impressive capabilities, LLMs are not without limitations. One of the most significant challenges facing LLMs today is the problem of inference speed. Due to the sheer size and complexity of these models, the process of making predictions or extracting information from them can be computationally expensive and time-consuming. Several ways to speed up the LLMs without updating hardware:

Customize a local chatbot in streamlit

4 minute read

Published:

Large Language Models (LLMs) are the brains of various chatbots, and luckily we all have access to some brilliant cheap or even free LLMs now, thanks to open source community. It is possible to run LLMs on a PC and keep everything local. This blog presents my solution to building a chatbot running on my PC, with a totally local file storage system and a costumized graphical user interface.